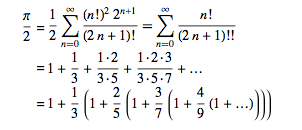Roy Berube
meanderings

Adventures in Calculating Pi

I blame Matt Parker and his YouTube channel ‘standupmaths’. Every year on Pi day he takes on the topic, and this managed to pique my interest in how the number is calculated.
Pi is an irrational number, which means it cannot be defined as a fraction and has no repeating sequence of numbers. The last time I checked, someone had calculated it to 4 trillion digits using a home computer. It took months.
A Brief History Lesson
There are two general ways to calculate the number: geometry or infinite series. The geometry method is intuitive but went out of fashion about 300-400 years ago. Methods based on infinite series - more precisely Taylor series - were developed as calculus was discovered by great thinkers such as Leibniz and Newton in the 17th century. Euler was another great mathematical thinker who came along afterwards and managed to improve the convergence rate of Leibniz’s formula.
The Implementation
My programming language of choice for this is C#. Not the fastest language for this, but is capable nonetheless. I started with a C# sample from Rosetta Code which was indecipherable to me. I still do not fully understand what is happening in that code - my goal became to understand the underlying technique and rewrite it.
The same page on Rosetta Code has links to source pages for the algorithm. A spigot technique is used, which means that the program will churn out digits as long as it runs. Interesting stuff.
The formula is based on Euler’s refinement:
Initially I implemented a spigot version based on a fraction class and while that version worked and was easy to read, it was painfully slow. The fraction class was clearly a huge bottleneck. Using what I had learned, I then wrote an optimized version based on fractions without the fraction class. Here is the code. To use it, instantiate the class and call the CalcPi() method.
using System;
using System.Numerics;
/// <summary>
/// Another implementation of Pi spigot.
/// Optimization for speed is the goal this time, while remaining readable.
/// Runs in about 2/3 the time compared to the method from Rosetta Code.
/// 10k=10s. 40k=2m23s. 100k=23minutes.
/// /// </summary>
class OptimizedPiSpigot
{
uint count;
// s/t is the series 1,1/3,2/5,3/7 and so on.
//Skip first number in series to simplify algorithm.
BigInteger s = 1;
BigInteger t = 3;
// u/v is the result fraction of each pass. Skip first number in series to simplify algorithm.
BigInteger u = 2;
BigInteger v = 1;
// Running total storage x/v. Spigot number is sliced off of x.
BigInteger x = 2;
// Spigot comparison numbers. Produce output only if they match.
BigInteger np = 0; // Highest possible result of future pass.
BigInteger nn = 1; // Result of current pass.
/// <summary>
/// Calculate a given length of Pi.
/// </summary>
/// <param name="digits"></param>
public void CalcPi(int digits = 20)
{
while (digits >= 0)
{
nn = GetMSD(x / v);
// To test if possible largest size of future u is big enough to influence the MSD of x/v.
np = GetMSD(((2 * u) + x) / v);
if (nn == np)
// Produce output digit.
{
Console.Write(nn);
// Lop off the MSD.
x = x - (v * nn);
CalcSeries();
x *= 10;
u *= 10;
digits--;
}
else
// Consume input step of Taylor series.
{
CalcSeries();
}
}
}
/// <summary>
/// Calculate the Taylor series.
/// </summary>
private void CalcSeries()
{
// Post increment s by 1 and t by 2 after the calc.
u = u * s++;
v = v * t;
// Calculate the running total.
x = x * t;
//y = y * t; // x/y we can ignore y and use x/v instead. x and u share the same base.
x += u;
t += 2;
}
/// <summary>
/// Get the MSD of I.
/// </summary>
/// <param name="I"></param>
/// <returns></returns>
private BigInteger GetMSD(BigInteger I)
{
while (I > 9)
{
I /= 10;
}
return I;
}
}
The reason to use fractions is that each step has absolute precision without the precision loss of using decimal numbers. Even in this optimized version the fraction values blow up immensely. Note the comments in the code for some timing measurements. Time required increases exponentially; I did not bother to try runs over 100k digits because of this.
I later experimented with some other algorithms in C# that are much quicker, but this is enough for now.
Written on July 24th, 2017 by Roy Berube